東海道本線の大津~京都間は、1880(明治13)年に開業したが、山科盆地を間にはさんでいたため、その南縁を大きく迂回していた。この区間には、延長664.8mの逢坂山トンネルが建設され、最急勾配は25‰であった。このため、箱根越え、関ヶ原越えと並ぶ東海道本線の難所となり、新路線を建設することとなった。
工事は、鉄道院神戸鉄道管理局(のち鉄道省神戸改良事務所)が担当し、1914(大正3)年12月に着工した。新線は、山科盆地の北縁を経由し、延長2325.5mの新逢坂山トンネルと延長1864.8mの東山トンネルを掘削してその中間に山科駅を設け、1921(大正10)年8月1日より新線の使用を開始した。
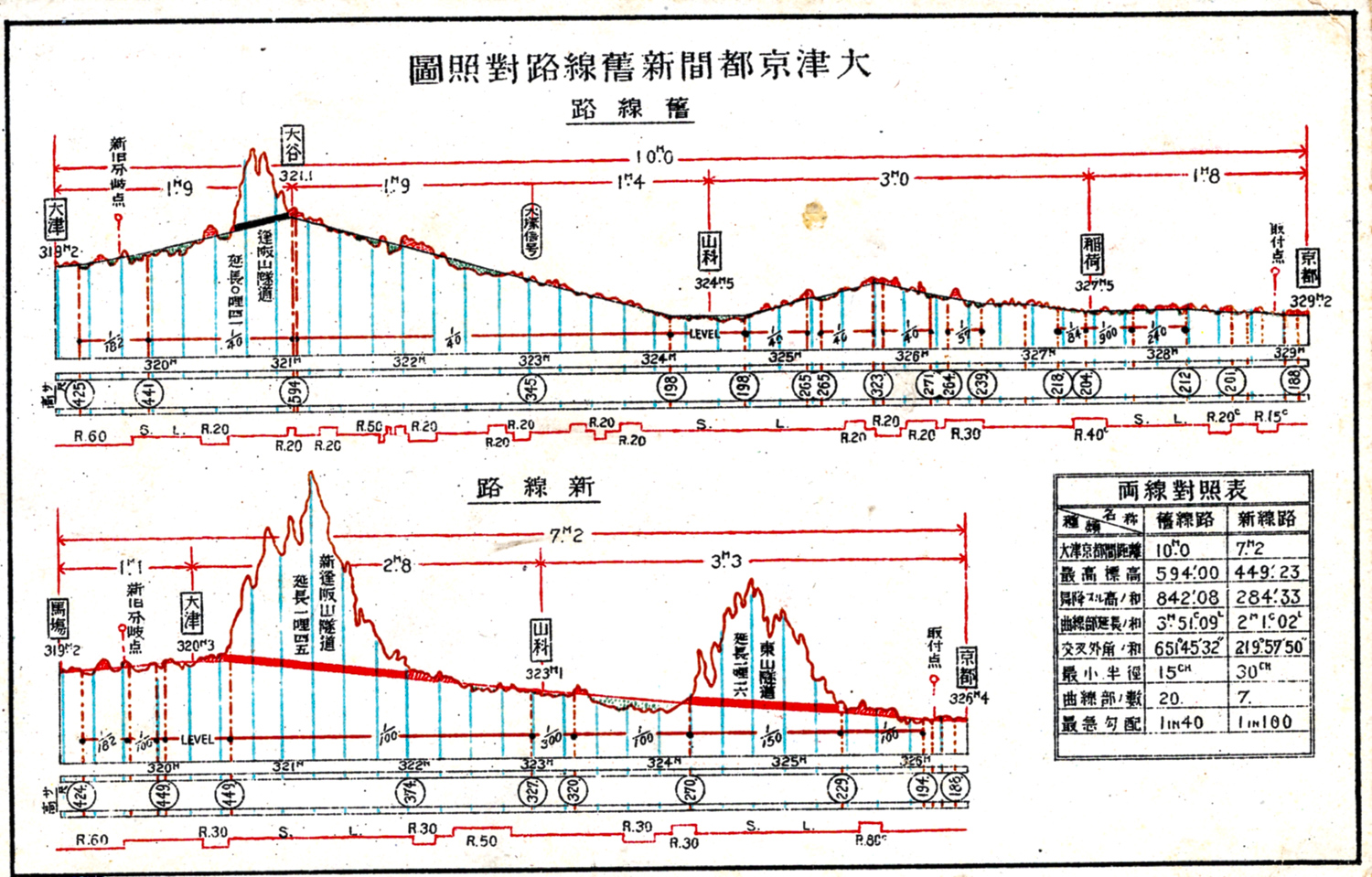
新線の開業を記念して鉄道省神戸改良事務所が発行した絵葉書には、旧線と新線の線路縦断面図が掲載され、あわせて改良工事の前後の諸元が「両線対照表」として比較された。この表によれば、大津~京都間の線路延長は10哩(約16.1km)から7.2哩(約5.6km)に短縮され、最急曲線は15鎖(約302m)から30鎖(約604m)に、最急勾配は10‰に緩和された。
路線の勾配改良工事は、路線の短絡による到達時間の短縮と、勾配の緩和による牽引定数の増加と速度向上という相乗効果をもたらした。改良工事の完成によって、大津~京都間の所要時間は約30~50分から15分前後に短縮された。東海道本線の勾配改良工事は、さらに丹那トンネルの建設による箱根越えの解消、別線による関ヶ原越えの解消と続き、昭和戦前期にはほぼ現在の姿を整えた。
なお、大津~京都間の線路変更工事によって廃止された旧線のうち、稲荷~京都間の線路敷は、奈良線へ編入して引き続き使用し、現在に至っている。(小野田滋)(「日本鉄道施設協会誌」2015年12月号掲載)
Q&A
「大津京都間新旧線路対照図」の見方を教えてください。
大津から京都までの線路の縦断面を比較した図で、横軸が水平距離、縦軸が標高を表していて、縦軸の縮尺を大縮尺として勾配を強調しています。地形の断面とトンネルの位置が図示され、下のスケールは上から勾配、哩程(東京起点の水平距離)、標高、曲線半径(R)を示しています。上が大津~京都間の改良工事前の線路縦断面図、下が改良工事後の線路縦断面図で、改良工事によって水平距離が短くなり、勾配も緩くなっていることがわかります。なお、距離の単位はマイルで示されていて、「M」が「マイル(哩):1.6093km」、「C/CH」が「チェーン(鎖):20.12m」、「L」が「リンク(節):201.2mm」という単位になります。また標高はフィート単位(1フィート=0.3048m)で、勾配は分子を1とした単位分数で表されています。(小野田滋)
”東海道本線・大津~京都間(滋賀県大津市/京都市東山区・山科区)”番外編
こうして比較すると、大津~京都間の距離が短くなって、勾配も緩くなっていることがよくわかりますね。
結果として到達間が短くなって、より重い貨物を運べることになる。
この時代はメートル単位ではなかったんですね。
日本の鉄道はイギリス人技師の指導でスタートしたこともあって、最初はマイルを単位に使っていた。
いつからメートル法に変わったんですか?
国としては1921(大正10)年の度量衡法の改正でメートル法に統一することが決まったんだが、なかなか完全実施には至らず、鉄道省では1928(昭和3)年にメートル法による設計示方書が制定されてから徐々に広まった。
勾配の単位も今使っているパーミル(‰)ではないですよ。
勾配の単位も1925(大正14)年の「線路諸標設備心得」の制定までは、単位分数で表していた。
ってことは、どの単位を使って設計したかがわかれば、設計した時代が把握できますね。
歴史的構造物も、メートル単位で寸法を測ると端数が出るが、フィート単位に換算すると切りのいい数値にまとまることがあるぞ。
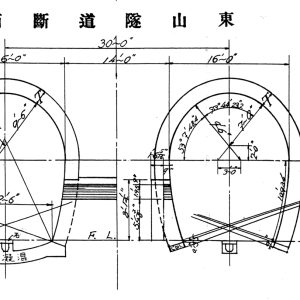
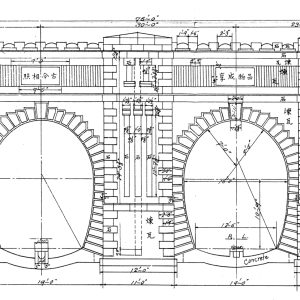
参考図にある東山トンネルの図面も、単位はフィートですか?
数字の右上の記号がプライム記号「′」だと「フィート」、ダブルプライム記号「″」だと「インチ」を表すことになるから、フィート単位の図面だ。
図面の世界も奥が深いですね。
図面は言葉では表すことができないさまざまな情報が詰まっているから、これを読み解くことが構造物を理解する第一歩だ。
師匠もたまにはいいこと言いますね。
「たまに」は余計だ💢